
피보나치 함수를 구현하는 문제이다. 하지만 일반적인 재귀함수를 이용하는 방법으로 풀면 시간 초과가 뜰 것이다.
이를 해결하기 위해서 동적 계획법에 대해 알아보자.
동적 계획법 (Dynamic Programming)이란,
하나의 복잡한 문제를 동일한 구조의 간단한 문제들의 합으로 푸는 방법이다. 하나의 문제를, 그것과 동일한 형태의 작은 문제들로 나눈 뒤, 작은 문제들을 풀어내어 최종적인 문제에 접근하는 것이 목적이다.
메모이제이션 (memoization)이란,
문제를 푸는 도중에, 여러개의 작은 문제들이 도출되는데, 이 문제들이 겹쳐지면 중복계산이 발생하여 시간이 오래 걸린다. 따라서, 한번 푼 문제는 중복하여 풀지 않도록 Cache를 저장해주는 작업을 해준다. 이를 메모이제이션이라고 한다.
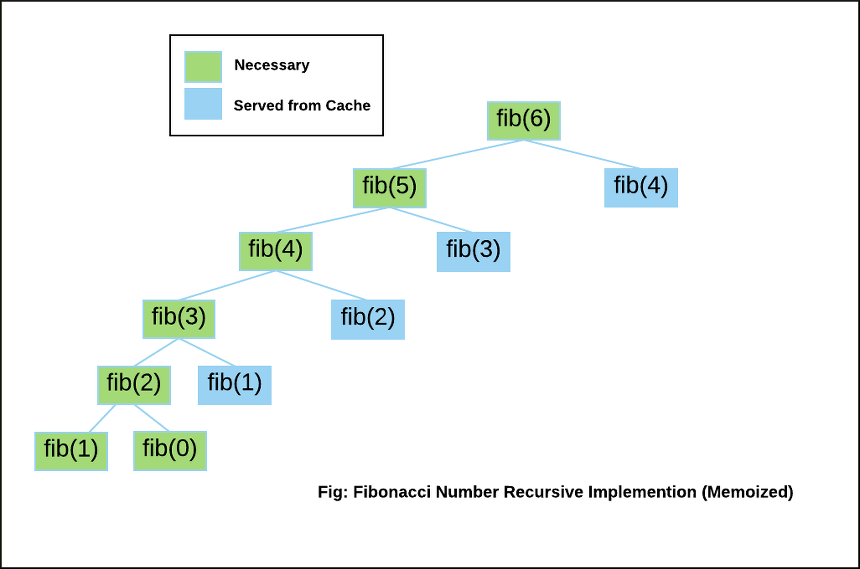
동적 계획법으로 문제를 풀 때, 2가지의 관점이 존재하는데,
1. 큰 문제에서 시작해서 아래로 푸는 Top-down
2. 작은 문제에서 시작해서 위로 푸는 Bottom-up 이다.
탑 다운(Top-down)
1. 큰 문제를 풀 때, 작은 문제를 계산하는 과정으로 빠진다.
2. 재귀 형태로 문제를 푼다.
3. 오버 플로우에 유의해야 한다.
바텁 업(Bottom-up)
1. 아래 단계부터 풀어서, 목표 단계까지 접근한다.
2. 반복문 형태로 문제를 푼다.
3. 점화식이 사용된다.
위의 특징들 외에도 다른 특징들이 있다.
각설하고, 이 문제를 풀 때는 기존의 재귀방식대로 풀면 안되기 때문에 Botton-up방식으로 풀어봤다.
fibo는 각 단계에서 구한 값을 메모이제이션하기 위해서 선언한 배열이고 하나의 테스트 케이스에서 사용했으면 del해서 삭제한 뒤 다시 선언했다.
##메인 함수 부분##
if __name__ == "__main__":
T = int(input()) #테스트 케이스
for i in range(T):
fibo = []
fibo.append(0)
fibo.append(1)
N = int(input())
j = 2 #j는 2부터 원하는 값을 구할 때까지 1씩 증가한다.
if N == 0:
print(' '.join(['1','0']))
elif N == 1:
print(' '.join(['0','1']))
else:
while True:
if j == N+1:
break
fibo.append(fibo[j-1] + fibo[j-2])
j += 1
print(' '.join([str(fibo[N-1]), str(fibo[N])]))
del(fibo)동적 계획법에 대해 알아보고 나면, 가로로 0 1 1 2 3 5 8 13 .. 식으로 쓰면서 배열에 하나하나 append해주면서 풀면 되겠다는 생각이 바로 들었다.
'백준 문제풀이(파이썬) > 동적 계획법 1' 카테고리의 다른 글
| 백준 2579번 - 계단 오르기 (0) | 2021.06.04 |
|---|---|
| 백준 1932번 - 정수 삼각형 (0) | 2021.06.02 |
| 백준 1149번 - RGB거리 (0) | 2021.06.01 |
| 백준 9461번 - 파도반 수열 (0) | 2021.06.01 |
| 백준 9184번 - 신나는 함수 실행 (0) | 2021.05.31 |
