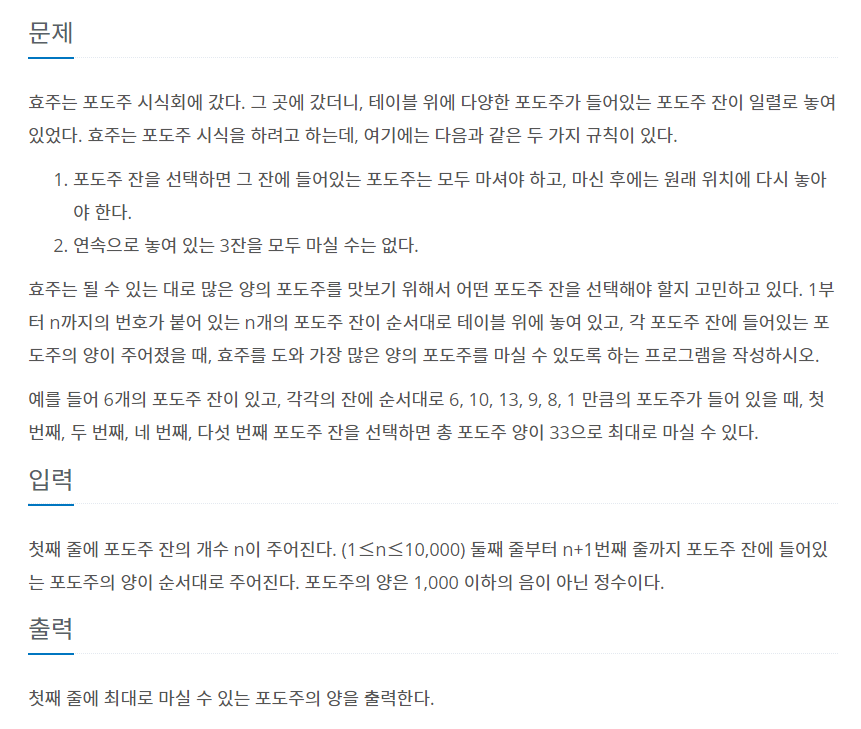
최대로 마실 수 있는 포도주의 양을 구하는 문제이다. 이 문제는 백준 2579번(계단 오르기)과 매우 유사하다.
백준 2579번 - 계단 오르기
계단을 오르면서 밟는 발판의 최댓값을 구하는 문제다. 이전에 풀었던 삼각형 문제나 집 색깔 문제처럼 뒤에서 차례대로 더하면서 갱신해주는 방식을 생각했지만, 경우가 깔끔하게 나뉘는 것도
aodtns.tistory.com
계단 문제에서 연속으로 세 칸을 밟을 수는 없는 것처럼 이 문제에서는 연속으로 3잔을 모두 마실 수는 없다. 계단 문제에서는 마지막 계단을 꼭 밟아야 했기 때문에, 마지막 계단을 밟기 전의 경우들의 최댓값을 구해서 비교해주었다. 반면에 이 문제는 그런 조건이 없기 때문에 경우를 새롭게 나눠줘야 한다.
case 1은 N번째 잔을 마시는 경우중에서 N-1번째 잔도 마시는 경우이다. 이 경우에는 N-2번째 잔을 마실 수 없기 때문에 N-3번째 잔까지의 최댓값에 N과 N-1번째 잔을 더해주면 된다.
case 2는 N번째 잔을 마시는 경우 중에서 N-1번째 잔을 마시지 않는 경우이다. 이 경우엔 N-2번째 잔까지의 최댓값에 N번째 잔을 더해주면 된다.
case 3는 N번째 잔을 마시지 않는 경우이다. 이 경우엔 N-1번째 잔을 꼭 마셔야 한다. N-1번째 잔을 마시지 않고 N-2번째 잔을 마신다면, N번째 잔을 마시지 않을 이유가 없기 때문이다.
그러므로 N-1번째 잔과 N-2번째 잔과 N-4번째 잔까지의 최댓값을 더해주면 된다.
##함수 선언 부분##
import sys
##변수 선언 부분##
grape = []
grape_max = []
case1 = 0
case2 = 0
case3 = 0
##메인 함수 부분##
if __name__ == "__main__":
N = int(input())
for i in range(N):
grape.append(int(input()))
grape_max.append(grape[0])
if N == 1:
print(grape_max.pop())
sys.exit(0)
grape_max.append(grape[1] + grape[0])
if N == 2:
print(grape_max.pop())
sys.exit(0)
grape_max.append(max((grape[0]+grape[1]),(grape[0]+grape[2]),(grape[1]+grape[2])))
if N == 3:
print(grape_max.pop())
sys.exit(0)
grape_max.append(max((grape[0]+grape[1]+grape[3]),(grape[0]+grape[2]+grape[3]),(grape[1]+grape[2])))
if N == 4:
print(grape_max.pop())
sys.exit(0)
for i in range(4,N):
case1 = grape_max[i-3] + grape[i-1] + grape[i]
case2 = grape_max[i-2] + grape[i]
case3 = grape_max[i-4] + grape[i-2] + grape[i-1]
grape_max.append(max(case1,case2,case3))
print(grape_max.pop())
계단 오르기 문제와 매우 유사해서 문제를 푸는 데 어려움을 느끼진 못했던 것 같다.
'백준 문제풀이(파이썬) > 동적 계획법 1' 카테고리의 다른 글
| 백준 11054번 - 가장 긴 바이토닉 부분 수열 (0) | 2021.06.12 |
|---|---|
| 백준 11053번 - 가장 긴 증가하는 부분 수열(LIS) (0) | 2021.06.11 |
| 백준 10844번 - 쉬운 계단 수 (0) | 2021.06.09 |
| 백준 1463번 - 1로 만들기 (0) | 2021.06.04 |
| 백준 2579번 - 계단 오르기 (0) | 2021.06.04 |
