문제를 풀기 전에 이번 단계의 주제인 그리디 알고리즘에 대해 알아보자.
Greedy Algorithm이란 문제를 해결하는 과정에서 그 순간마다 최적이라고 생각되는 결정을 하여 최종 해답에 도달하는 문제 해결 방식이다.
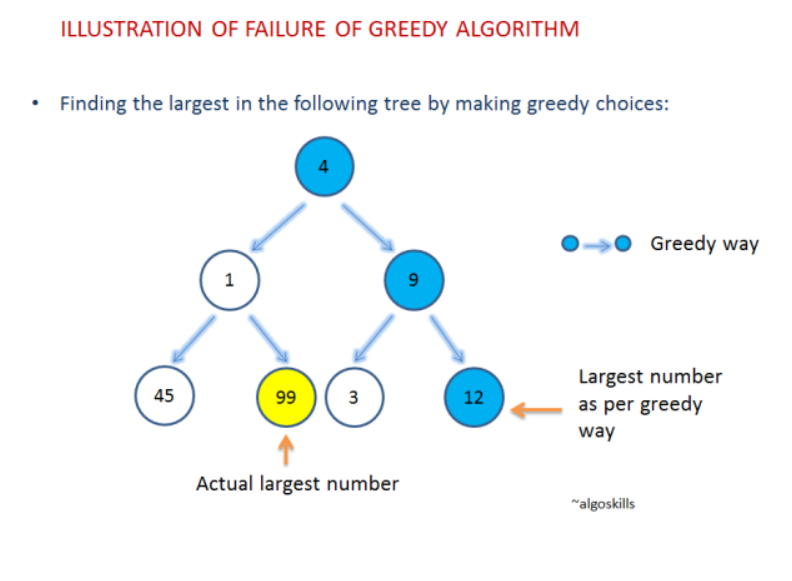
위 그림은 가장 큰 수를 찾는 문제인데, 매 순간순간마다 큰 값을 찾아나가면 엉뚱한 결과가 나온다. 다시말해, 그리디 알고리즘이 항상 전체 문제해결에서 최적의 해답을 찾지는 못한다는 것이다. 그렇다면 왜 이 알고리즘을 사용할까?
그리디 알고리즘은의 가장 큰 장점은 계산 속도에 있다. DP는 모든 경우를 탐색하지만 계산 속도가 느리고 그리디는 모든 경우를 탐색하지는 못하지만 계산 속도가 무척 빠르다. 그래서 DP와 그리디는 상호 보완하는 개념으로 알려져 있다.
또한 그리디 알고리즘은 Greedy choice property 와 Optimal Substructure 조건을 성립해야 잘 작동한다.
전자는 앞의 선택이 이후의 선택에 영향을 주지 않는다는 조건이고, 후자는 문제에 대한 최종 해결 방법이 부분 문제에 대해서도 또한 최적 문제 해결 방법이다는 조건이다.
이 문제에 그리디 알고리즘을 적용해보자. 먼저 배열을 돌면서 매 순간마다 최적의 조건을 찾아가면 되겠다. 만약 처음부터 터무니 없는 큰 숫자가 나온다고 생각하면 그냥 무작정 그리디 알고리즘을 적용했을 때 오답이 나올 것이다. 또한 시작 시간과 종료시간이 같은 경우도 있기 때문에, 종료 시간이 가장 작은 순서대로 정렬을 한 뒤에 시작 시간이 작은 순서로 정렬을 해주면 된다.
##변수 선언 부분##
data = []
sum = 1
##메인 함수 부분##
if __name__ == "__main__":
N = int(input())
data = [[int(x) for x in input().split()]for y in range(N)]
data.sort(key=lambda x: (x[1],x[0])) #끝나는 시간으로 오름차순 정렬하고 같으면 시작하는 시간으로 정렬
end = data[0][1] #첫 번째값의 끝나는 시간을 저장
for i in range(1,N):
if data[i][0] >= end: #앞의 회의가 끝나는 시간보다 뒤에 시작하면
sum += 1 #sum증가
end = data[i][1] #회의 끝나는 시간 갱신
print(sum)그리디 알고리즘에 대해 공부하지 않으면 쉽게 다가가기 힘든 문제였다.
'백준 문제풀이(파이썬) > 그리디 알고리즘' 카테고리의 다른 글
| 백준 13305번 - 주유소 (0) | 2021.06.19 |
|---|---|
| 백준 1541번 - 잃어버린 괄호 (0) | 2021.06.18 |
