이전까지는 생선들의 종류를 분류하는 모델, 길이를 이용해 무게를 예측하는 모델, 특정 생선일 확률을 예측하는 모델 등을 설계했었다. 이번엔 캔 와인을 예시로 들어 캔에 인쇄되어있는 도수, 당도, pH 값으로 화이트 와인인지 레드 와인인지를 분류해보자.
분류를 시작하기 전에 생각해보면 길이와 무게 등의 데이터로 빙어인지 도미인지 구분하는 모델을 설계했었기 때문에 와인을 분류하는 것 또한 쉽게 해결할 수 있을 것 같다.
로지스틱 회귀를 이용한 와인 분류
일단 데이터셋을 불러와서 head() 메서드로 처음 5개의 샘플을 확인해보자.
import pandas as pd
wine = pd.read_csv('https://bit.ly/wine_csv_data')
wine.head()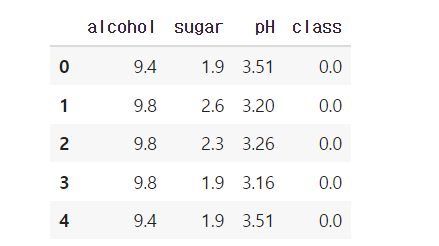
데이터셋에는 알코올 도수, 당도, pH 값이 들어있고 네 번째 열 class는 타깃값인데 0이면 레드 와인, 1이면 화이트 와인이다. 레드 와인인지 화이트 와인인지 분류하는 것은 이진 분류이고 화이트 와인이 양성 클래스이다. 다시 말해, 이 문제는 전체 와인 데이터에서 화이트 와인을 골라내는 문제이다.
판다스 데이터프레임에는 유용한 메서드 2개가 있는데, info() 메서드와 describe() 메서드이다.
info() 메서드는 데이터프레임의 각 열의 데이터 타입과 누락된 데이터가 있는지 확인하는 데 유용하다.
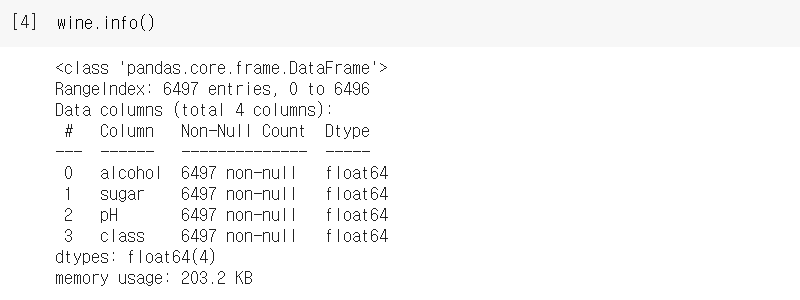
총 6497개의 샘플이 있고 4개의 열은 모두 실숫값이다. 또한 Non-Null Count 값이 6497이므로 누락된 값은 없다.
만약 누락된 값이 있다면 그 데이터를 버리거나 평균값으로 누락된 값을 채워서 사용할 수 있다. 어떤 방식이 좋은지는 미리 알기 어렵기 때문에 모두 시도해보는 것이 좋다.
decribe() 메서드는 열에 대한 간략한 통계를 출력해준다. 간략한 통계라함은 최소, 최대, 평균값 등을 볼 수 있다.
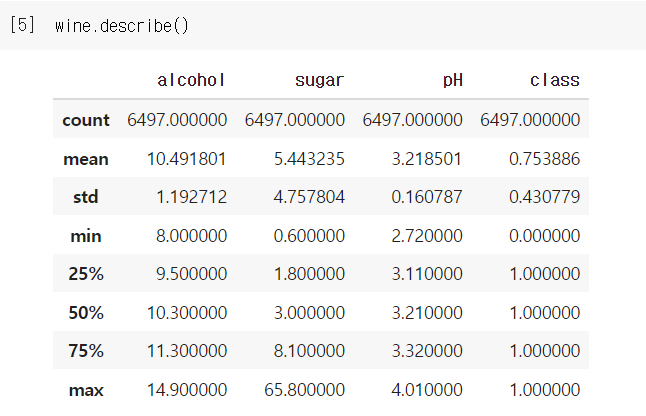
25%, 50%, 75%는 각각 1사분위수, 중간값, 3사분위수를 의미한다. 사분위수는 데이터를 순서대로 4등분 한 값이다. 예를 들어 2사분위수(중간값)은 데이터를 일렬로 늘어놓았을 때 정중앙의 값이다. 데이터가 짝수면 가운데 2개 값의 평균을 사용한다.
위의 표에서 알 수 있는 것은 도수, 당도, pH 값의 스케일이 다르다는 것이다. 그러므로 StandardScaler 클래스로 특성을 표준화해야한다. 판다스 데이터프레임을 넘파이 배열로 바꾸고 훈련 세트와 테스트 세트로 나누자.
from sklearn.model_selection import train_test_split
train_input, train_target, test_input, test_target = train_test_split(
data, target, test_size = 0.2, random_state = 42
)train_test_split() 함수는 설정값을 지정하지 않으면 25%를 테스트 세트로 지정한다. 샘플 개수가 충분히 많기 때문에 test_size = 0.2로 설정하여 20% 정도만 테스트 세트로 나눴다.
StandardScaler 클래스를 사용하여 훈련 세트를 전처리해보자.
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
데이터 준비가 끝났으니 표준점수로 변환된 train_scaled와 test_scaled를 사용하여 로지스틱 회귀 모델을 훈련하자.
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_scaled, train_target)
점수가 높지는 않은 것을 보아하니 생각보다 화이트 와인을 골라내는 것이 어려운 것같다. 두 세트의 점수가 모두 낮으니 모델이 다소 과소적합된 것 같다. 규제 매개변수 C의 값을 바꿔서 점수를 높일 수 있을까? 아니면 solver 매개변수에서 다른 알고리즘을 선택해야할까? 다항 특성을 만들어서 추가할 수도 있겠다.
로지스틱 회귀가 학습한 계수와 절편을 출력해보자.

이 모델은 도수에 0.512~를 곱하고 당도에 1.67~을 곱하고 pH에 -0.687~을 곱한 다음 모두 더하고 1.81~까지 더하여 이 값이 0보다 크면 화이트 와인, 작으면 레드 와인으로 분류한다. 약 77퍼센트 정도를 정확히 화이트 와인으로 분류했다.
우리는 모델이 왜 저런 계수 값을 학습했는지 알기 어렵다. 또한 정확히 이 숫자가 어떤 의미인지 설명하기 어렵다. 다항 특성을 추가한다면 설명하기가 더 어려울 것이다. 쉬운 방법으로 설명할 수 있는 모델이 없을까?
결정 트리(Decision Tree)
결정 트리는 스무고개와 비슷한데 데이터를 잘 나눌 수 있는 질문을 추가해서 분류의 정확성을 높이는 느낌이랄까.
사이킷런의 DecisionTreeClassifier 클래스를 사용하여 결정 트리 모델을 훈련해보자.
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(random_state=42)
dt.fit(train_scaled, train_target)
훈련 세트에 대한 점수가 매우 높지만 테스트 세트에 대한 점수가 조금 낮다. 과대 적합된 모델이라고 봐야될 것 같다. 사이킷런의 plot_tree() 함수를 사용하여 결정 트리를 이해하기 쉬운 트리 그림으로 출력해보자.
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
plt.figure(figsize=(10,7))
plot_tree(dt)
plt.show()
상당히 복잡해보이는 트리가 출력이 된다. 트리의 깊이를 제한해서 출력하려면 max_depth 매개변수를 이용하면 된다.
max_depth 매개변수를 1로 주면 루트 노드를 제외하고 하나의 노드를 더 확장해서 그린다는 뜻이다. filled 매개변수로 클래스에 맞게 노드의 색을 칠할 수 있고 feature_names 매개변수로 특성의 이름을 전달할 수 있다. 이 매개변수들을 사용하여 좀 더 잘 보이게 트리를 출력해보자.
plt.figure(figsize=(10,7))
plot_tree(dt, max_depth=1, filled=True, feature_names=['alcohol','sugar','pH'])
plt.show()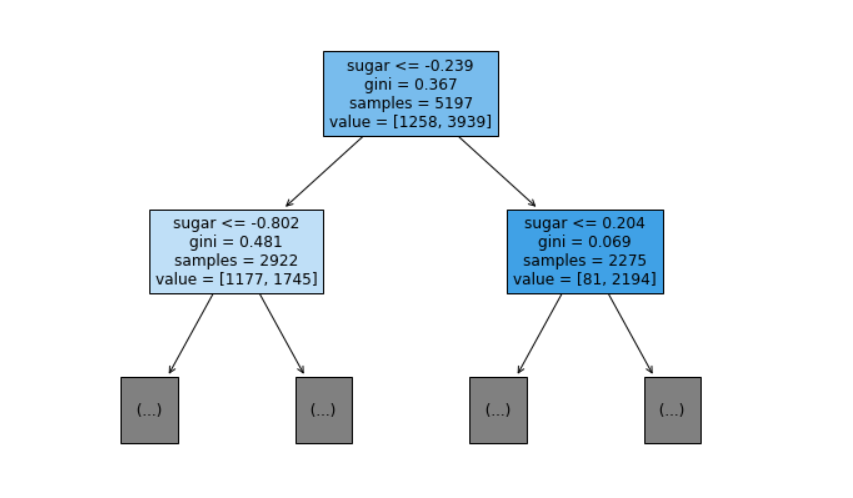
뜻을 살펴보자. 루트 노드는 당도가 -0.239보다 같거나 작으면 왼쪽 가지로 간다. 그렇지 않으면 오른쪽 가지로 간다.
왼쪽이 Yes이고 오른쪽이 No이다. 루트 노드의 총 샘플 개수는 5197개이다. 이 중에서 음성 클래스(레드 와인)는 1258개 양성 클래스(화이트 와인)는 3939개이다. 왼쪽 노드로 넘어가보면 이 노드는 당도가 더 낮은지(-0.802보다 낮은지) 물어본다. 노드의 색깔은 어떤 클래스의 비율이 높아질수록 진해진다. 루트 노드는 양성 클래스의 비율이 더 높아서 진한 하늘색이고 왼쪽 노드는 비율이 비슷해서 하늘색, 오른쪽 노드는 양성 클래스의 비율이 매우 높아서 진한 파란색을 띈다.
결정 트리에서 클래스르 예측하는 방법은 간단하다. 리프 노드에서 더 많은 클래스가 예측 클래스가 된다. 만약 위의 노드 세개로 끝이 난다면 세 노드가 모두 양성 클래스가 더 많기 때문에 예측 클래스는 양성 클래스일것이다.
지니 불순도(Gini Impurity)
위의 노드 안의 gini는 지니 불순도(Gini Impurity)를 의미한다. DecisionTreeClassifier 클래스의 criterion 매개변수의 기본값이 gini인데, criterion 매개변수의 용도는 노드에서 데이터를 분할할 기준을 정하는 것이다. 앞에서 루트노드의 기준을 당도로 나눌 때 어떻게 -0.239를 기준으로 나눴을까? 바로 criterion 매개변수에 지정한 지니 불순도때문이다. 지니 불순도는 클래스의 비율을 제곱해서 더한 다음 에서 빼면 된다.
지니 불순도 = 1 - ( (음성 클래스 비율)² + (양성 클래스 비율)² )
다중 클래스 문제여도 계산 방법은 같다. 루트 노드의 지니 불순도를 계산해보자.
1 - ((1258 / 5197)² + (3939 / 5197)²) = 0.367
노드에 하나의 클래스만 있다면 지니 불순도는 0이 되어 가장 작다. 이런 노드를 순수 노드라고 한다.
결정 트리 모델은 부모 노드와 자식 노드의 불순도 차이가 가능한 크도록 트리를 성장시킨다. 부모 노드와 자식 노드의 불순도 차이는 다음 식으로 계산한다.
부모의 불순도 - (왼쪽 노드 샘플 수 / 부모의 샘플 수) x 왼쪽 노드 불순도 - (오른쪽 노드 샘플 수 / 부모의 샘플 수) x 오른쪽 노드 불순도 = 0.367 - (2922 / 5197) x 0.481 - (2275 / 5197) x 0.069 = 0.066
이런 부모와 자식 노드 사이의 불순도 차이를 정보 이득(information gain)이라고 한다. 결정 트리 알고리즘은 정보 이득이 최대가 되도록 데이터를 나눈다.
DecisionTreeClassifier 클래스에서 criterion='entropy'로 지정하여 엔트로피 불순도를 사용할 수 있다. 엔트로피 불순도의 계산은 하지 않겠다. 결과의 차이가 크지 않으니 기본값인 지니 불순도를 사용하자.
가지치기
백트레킹에서의 가지치기처럼 결정 트리도 가지치기를 해야한다. 그렇지 않으면 무작정 끝까지 자라나는 트리가 만들어진다. 이렇게 만들어진 트리는 훈련 세트에 과대적합되어 테스트 세트에서의 점수가 매우 낮을것이다. 이를 일반화가 잘 안 될 것 같다고 한다.
가지치기의 가장 간단한 방법은 max_depth 매개변수로 트리의 최대 깊이를 지정하는 것이다. 이렇게 하면 루트 노드 아래로 최대 3개의 노드까지만 성장할 수 있다.
dt = DecisionTreeClassifier(max_depth=3, random_state=42)
dt.fit(train_scaled, train_target)
훈련 세트의 성능은 낮아졌지만 테스트 세트의 성능은 거의 그대로이다. 트리를 그려보자.
plt.figure(figsize=(20,15))
plot_tree(dt,filled=True,feature_names=['alcohol','sugar','pH'])
plt.show()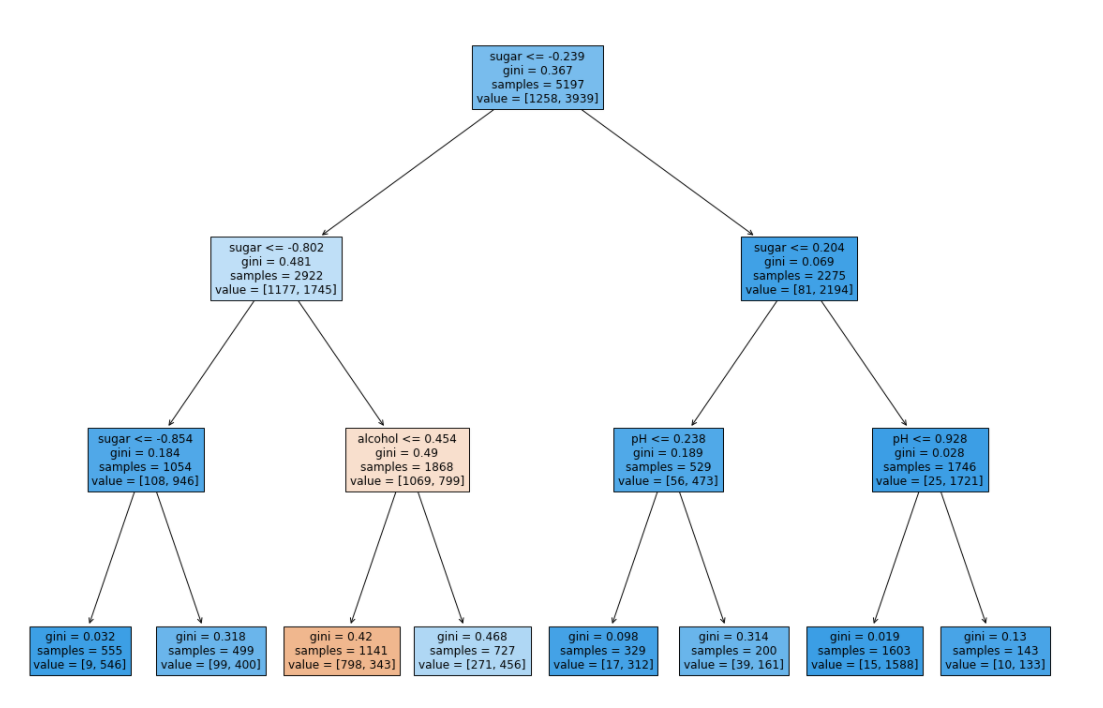
리프 노드들을 보면 왼쪽에서 세 번째 노드만 음성 클래스가 더 많다. 즉 위에서부터 조건에 맞게 내려와서 이 노드에 도착해야만 음성 클래스로 분류가 된다. 다시 말해 당도가 -0.802보다 크고, -0.239보다 작은 와인 중에 알코올 도수가 0.454와 같거나 작은 것이 레드 와인이다.
그런데 당도가 어떻게 -0.802라는 음수로 나타난 것일까? 앞에서 샘플을 나눌 때 불순도를 기준으로 나눈다고 하였다. 불순도는 클래스별 비율을 가지고 계산을 한다. 샘플을 어떤 클래스 비율로 나누는지 계산할 때 특성값의 스케일이 계산에 영향을 미치지 않기때문에 표준화 전처리를 할 필요가 없다. 이것이 결정 트리 알고리즘의 또 다른 장점 중 하나이다.
전처리 하기 전의 훈련 세트와 테스트 세트로 점수를 출력해보자.
dt = DecisionTreeClassifier(max_depth=3, random_state=42)
dt.fit(train_input, train_target)
결과가 같은 것을 확인할 수 있다.
plt.figure(figsize=(20,15))
plot_tree(dt,filled=True,feature_names=['alcohol','sugar','pH'])
plt.show()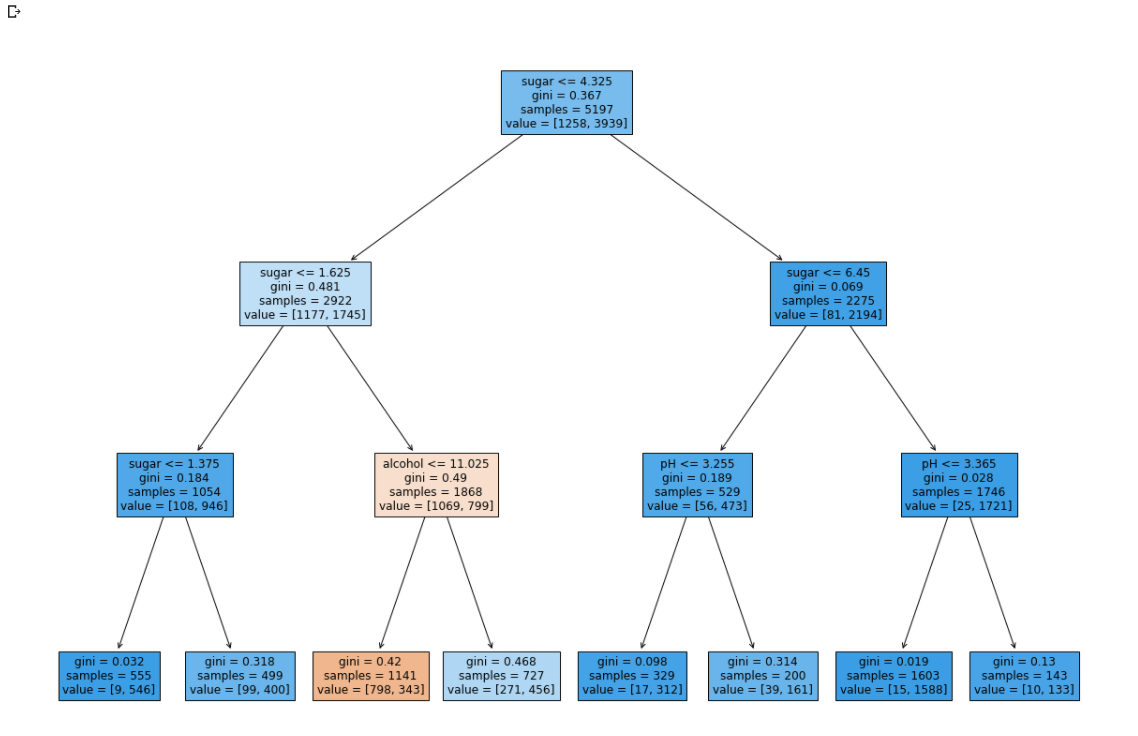
같은 트리지만 특성값을 표준점수로 바꾸지 않아서 이해하기 훨씬 쉽다.
결정 트리는 어떤 특성이 가장 유용한지 나타내는 특성 중요도를 계산해준다. 이 트리의 루트 노드와 깊이 1에서 당도를 사용했기 때문에 아마 당도가 가장 유용한 특성 중 하나일 것이다. 특성 중요도는 결정 트리 모델의 feature_importances_ 속성에 저장되어 있다.

두 번째 특성인 당도의 특성 중요도가 가장 높은 것을 확인할 수 있다. 특성 중요도는 각 노드의 정보 이득과 전체 샘플에 대한 비율을 곱한 후 특성별로 더하여 계산한다.
'AI > 머신 러닝(ML)' 카테고리의 다른 글
| 트리의 앙상블 (0) | 2021.08.21 |
|---|---|
| 교차 검증과 그리드 서치(Cross Validation & Grid Search) (0) | 2021.08.18 |
| 확률적 경사 하강법 (Stochastic Gradient Descent) (0) | 2021.08.14 |
| 로지스틱 회귀 (Logistic Regression) (0) | 2021.08.11 |
| 특성 공학과 규제 (0) | 2021.08.09 |
