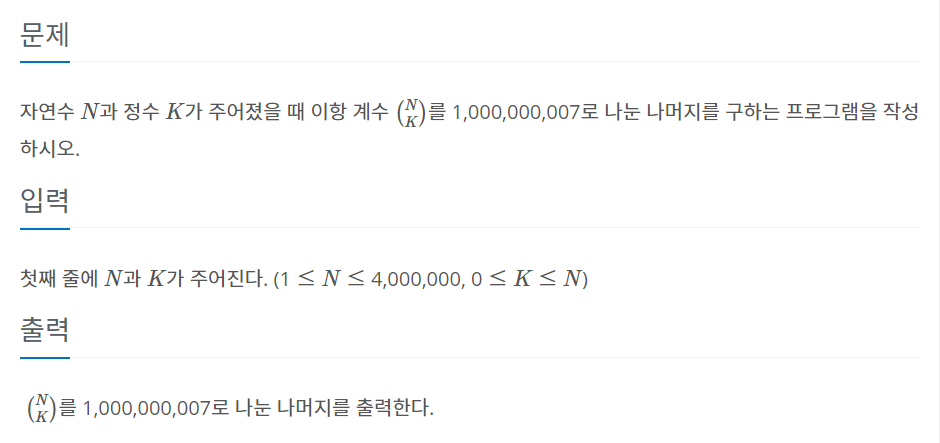
이항 계수를 구하는 문제이다. 이항 계수 1과 이항 계수 2에서는 DP로 풀 수 있었지만, 이 문제의 입력 범위가 매우 크기때문에 같은 방식으로 풀면 시간 초과가 뜬다. 그러므로 문제 앞에 나와있는 페르마의 소정리를 이용하여 풀어보자.
<페르마의 소정리>
정수 a와 p가 있고 a가 p의 배수가 아니면서 p가 소수(Prime number)일 때 다음이 성립한다.

수식을 풀이하면 a^p를 p로 나눈 나머지는 a를 p로 나눈 나머지가 된다는 뜻이다.
또한 양 변을 a로 나누면 다음 식을 유도할 수 있다.

(n, k)%p -> (n!/k!(n-k)!)%p
-> A=n!, B=k!(n-k)!로 치환
-> (A*B^(-1))%p
-> ((A%p) * (B^(-1)%p))%p
-> ((A%p) * (B^(p-2))%p)%p
-> (A*B^(p-2))%p
이로써 우리는 이항 계수를 분수가 아니라 두 정수의 곱으로 나타낼 수 있다. 또한 B의 거듭제곱은 분할 정복 거듭제곱으로 구하면 된다.
##함수 선언 부분
def mult(a,b):
if b == 1:
return a % p
tmp = mult(a,b//2)
if b % 2 != 0:
return ((tmp ** 2) * a) % p
else:
return (tmp ** 2) % p
##변수 선언 부분
p = 1000000007
fact = [1]*40000002
##메인 함수 부분
if __name__ == "__main__":
N, K = map(int, input().split())
#A = n!, B = K!(n-k)!
for i in range(2,N+1):
fact[i] = (fact[i-1] * i) % p
A = fact[N]; B = fact[K] * fact[N-K]
B_P_2 = mult(B,p-2)
print((A%p * B_P_2%p)%p)
페르마의 소정리를 모르면 풀 수 없는 문제였다.
'백준 문제풀이(파이썬) > 분할 정복' 카테고리의 다른 글
| 백준 6549번 - 히스토그램에서 가장 큰 직사각형 (분할 정복 풀이) (0) | 2021.08.03 |
|---|---|
| 백준 11444번 - 피보나치 수 6 (0) | 2021.08.01 |
| 백준 2630번 - 색종이 만들기 (0) | 2021.07.21 |

이항 계수를 구하는 문제이다. 이항 계수 1과 이항 계수 2에서는 DP로 풀 수 있었지만, 이 문제의 입력 범위가 매우 크기때문에 같은 방식으로 풀면 시간 초과가 뜬다. 그러므로 문제 앞에 나와있는 페르마의 소정리를 이용하여 풀어보자.
<페르마의 소정리>
정수 a와 p가 있고 a가 p의 배수가 아니면서 p가 소수(Prime number)일 때 다음이 성립한다.

수식을 풀이하면 a^p를 p로 나눈 나머지는 a를 p로 나눈 나머지가 된다는 뜻이다.
또한 양 변을 a로 나누면 다음 식을 유도할 수 있다.

(n, k)%p -> (n!/k!(n-k)!)%p
-> A=n!, B=k!(n-k)!로 치환
-> (A*B^(-1))%p
-> ((A%p) * (B^(-1)%p))%p
-> ((A%p) * (B^(p-2))%p)%p
-> (A*B^(p-2))%p
이로써 우리는 이항 계수를 분수가 아니라 두 정수의 곱으로 나타낼 수 있다. 또한 B의 거듭제곱은 분할 정복 거듭제곱으로 구하면 된다.
##함수 선언 부분
def mult(a,b):
if b == 1:
return a % p
tmp = mult(a,b//2)
if b % 2 != 0:
return ((tmp ** 2) * a) % p
else:
return (tmp ** 2) % p
##변수 선언 부분
p = 1000000007
fact = [1]*40000002
##메인 함수 부분
if __name__ == "__main__":
N, K = map(int, input().split())
#A = n!, B = K!(n-k)!
for i in range(2,N+1):
fact[i] = (fact[i-1] * i) % p
A = fact[N]; B = fact[K] * fact[N-K]
B_P_2 = mult(B,p-2)
print((A%p * B_P_2%p)%p)
페르마의 소정리를 모르면 풀 수 없는 문제였다.
'백준 문제풀이(파이썬) > 분할 정복' 카테고리의 다른 글
| 백준 6549번 - 히스토그램에서 가장 큰 직사각형 (분할 정복 풀이) (0) | 2021.08.03 |
|---|---|
| 백준 11444번 - 피보나치 수 6 (0) | 2021.08.01 |
| 백준 2630번 - 색종이 만들기 (0) | 2021.07.21 |
