
행렬의 제곱을 이용하여 피보나치수열을 구하는 문제이다. 피보나치 수를 구하는 방법 중에 DP를 이용하는 방법이 가장 효율적이라고 생각했었는데, 더 빠른 방법이 있다는 것이 신기했다. 일단 입력값이 매우 크기 때문에 O(N)의 알고리즘으로는 절대 풀 수 없음을 인지하고 있어야 한다. DP로 풀면 O(N)이기 때문에 다른 방법으로 풀어야 하는데, 앞에서 계속 풀었던 행렬을 이용하면 된다.
피보나치수열을 행렬을 이용하여 표현하면 밑의 식과 같다.
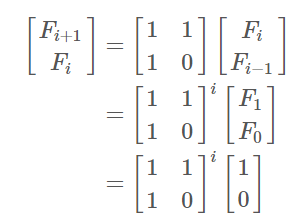
위의 식이 의미하는 것은 행렬 [[1,1], [1,0]]을 i번 제곱한 값에 행렬 [[1], [0]]을 곱하여 피보나치 수를 구할 수 있다는 것이다. 또한 제곱을 해줄 때 매번 1/2로 단축이 되기 때문에 시간 복잡도는 O(logN)이다.
##함수 선언 부분
MAX_NUM = 1000000007
def mult_mat(A, B): #행렬 A와 B의 곱 반환
C = [[0, 0], [0, 0]]
for i in range(2):
for j in range(2):
for k in range(2):
C[i][j] += (A[i][k] % MAX_NUM * B[k][j] % MAX_NUM) % MAX_NUM
return C
def Fibo(A, N):
if N == 1:
for i in range(2): #나머지 연산
for j in range(2):
A[i][j] = A[i][j] % MAX_NUM
return A
else:
ttmp = Fibo(A, N // 2)
if N % 2 == 0:
return mult_mat(ttmp, ttmp)
else:
return mult_mat(mult_mat(ttmp,ttmp), A)
##변수 선언 부분
A = [[1, 1], [1, 0]]
B = [[1],[0]]
##메인 함수 부분
if __name__ == "__main__":
N = int(input())
tmp = Fibo(A, N)
_C = [[0], [0]]
for i in range(2):
for j in range(2):
_C[i][0] += (tmp[i][j] % MAX_NUM * B[j][0] % MAX_NUM) % MAX_NUM
print(_C[1][0])어렵지 않은 문제였지만, 행렬의 제곱을 이용하는 문제인지를 몰랐다면 풀 수 없었을 것 같다.
'백준 문제풀이(파이썬) > 분할 정복' 카테고리의 다른 글
| 백준 6549번 - 히스토그램에서 가장 큰 직사각형 (분할 정복 풀이) (0) | 2021.08.03 |
|---|---|
| 백준 11401번 - 이항 계수 (0) | 2021.07.27 |
| 백준 2630번 - 색종이 만들기 (0) | 2021.07.21 |
