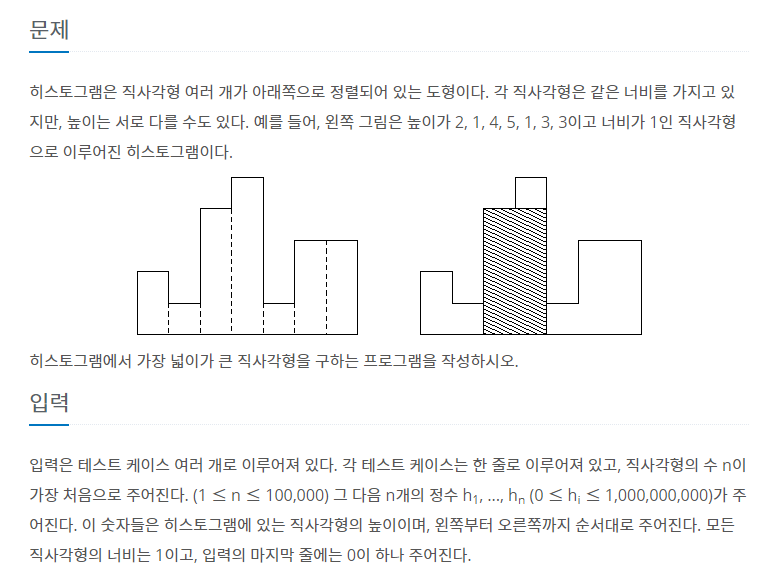
히스토그램에서 넓이가 가장 큰 직사각형을 구하는 문제이다. 최댓값이 될 수 있는 경우는
1. 경계의 왼쪽에서 너비 1의 직사각형이 최대인 경우
2. 경계의 오른쪽에서 너비 1의 직사각형이 최대인 경우
3.경계를 기준으로 붙어있는 직사각형이 최대인 경우로 세가지가 있다.
1번과 2번 경우는 너비가 1이 될 때까지 분할해서 1이면 높이를 return해주면 되지만, 3번 경우는 combine해줄 때 start부터 end까지 돌면서 최대의 직사각형을 구해줘야하기 때문에, 3번의 경우에 주목해서 코드를 짜야한다.
start부터 end까지의 범위가 정해졌을 때 경계(mid)를 기준으로 맞닿아있는 직사각형은 각각 square[mid](왼쪽), square[mid+1](오른쪽)일 것이다. left와 right는 각각 mid와 mid+1을 시작으로 start와 end까지 이동할 것이다.
이동할 때는 이동할 index의 값이 큰 쪽으로 먼저 이동할 것이다. 즉, square[left-1] > square[right+1]이라면 left로 이동하는 것이 최댓값을 찾을 확률이 높기 때문이다. 어디로 먼저 이동하는지는 상관이 없다.
left가 right보다 먼저 start까지 이동했다면, 남은 right를 end까지 이동시키면서 직사각형의 넓이를 구하고, right가 end까지 이동했다면, 남은 left를 start까지 이동시키면서 직사각형의 최대 넓이를 구한다. start부터 end까지 이동하면서 구한 직사각형의 최대 넓이, 경우 1, 2 중에 최댓값을 return해주면 된다.
##함수 선언 부분
def divide_square(square, start, end):
if start == end:
return square[start]
else:
mid = (start + end) // 2
cnt = 2 #너비를 의미한다
left = mid #경계 왼쪽
right = mid+1 #경계 오른쪽
min_tmp = min(square[left], square[right]) #둘 중에 작은 값을 min_tmp에 넣어준다.
tmp = min_tmp * 2 #너비에 min_tmp를 곱한 값이 경계를 사이에 두고 정해지는 직사각형의 크기
while True:
if (square[left] == 0 or left == start) and (square[right] == 0 or right == end):
#(왼쪽 경계의 값이 0이거나 더 이상 왼쪽으로 이동할 수 없고) (오른쪽 경계의 값이 0이거나 더 이상 오른쪽으로 이동할 수 없는 경우)
#반복문 탈출
break
elif square[left] == 0 or left == start: #왼쪽 경계의 값이 0 이거나 제일 왼쪽으로 모두 이동한 경우
if square[right + 1] < min_tmp: #경계 오른쪽으로 이동하는데, 만약 min_tmp보다 값이 작아야 갱신해준다.
min_tmp = square[right + 1]
right += 1
elif square[right] == 0 or right == end: #위의 경우와 반대로 이미 제일 오른쪽으로 모두 이동한 경우
if square[left - 1] < min_tmp:
min_tmp = square[left - 1]
left -= 1
else: #왼쪽 혹은 오른쪽으로 모두 이동할 수 있는 경우
if square[left - 1] > square[right + 1]: #왼쪽으로 이동시의 값이 더 크면
if square[left - 1] < min_tmp: #위와 마찬가지로 min_tmp보다 작은 경우만 갱신해준다.
min_tmp = square[left - 1]
left -= 1
else:
if square[right + 1] < min_tmp:
min_tmp = square[right + 1]
right += 1
cnt += 1 #이동할 때마다 너비 1 증가
tmp = max(tmp, min_tmp * cnt) #이전의 tmp와 min_tmp에 너비를 곱한 값 중에 큰 값을 tmp에 저장해준다.
return max(divide_square(square, start, mid), divide_square(square, mid+1, end), tmp)
##변수 선언 부분
histo = []
##메인 함수 부분
if __name__ == "__main__":
while True:
histo = list(map(int, input().split()))
if histo[0] == 0:
break
print(divide_square(histo, 1, len(histo)-1))서로 붙어있는 직사각형의 넓이너비 1의 직사각형이 하나씩 붙을 때마다 변하는 최댓값을 구하는 느낌이라 동적 계획법으로 풀어보려했지만, 고려해야할 변수가 너무 많아서 포기했다. 분할 정복 파트의 문제이기 때문에 무작정 합병 정렬처럼 mid를 구해 너비가 1이될 때까지 분할을 했지만, 다시 합병을 해줄 때 서로 합병되면서 생길 수 있는 최댓값을 처리할 방법이 생각나지 않았다. 구글링을 하여 서로 합쳐질 때의 최댓값을 구하는 법을 알아낸 뒤 풀었던 문제이다.
푸는 방법을 알기 전에는 매우 어렵게 느껴졌지만, 막상 풀어보니 충분히 풀 수 있었다고 생각한다. 는 무슨 플레 이상의 난이도에 벽을 느끼게 된 문제이다. 구글링 없이 혼자 힘으로는 풀기 어려웠던 문제.
'백준 문제풀이(파이썬) > 분할 정복' 카테고리의 다른 글
| 백준 11444번 - 피보나치 수 6 (0) | 2021.08.01 |
|---|---|
| 백준 11401번 - 이항 계수 (0) | 2021.07.27 |
| 백준 2630번 - 색종이 만들기 (0) | 2021.07.21 |
