이전 챕터의 데이터 전처리를 통해 길이와 무게 데이터로 도미인지 빙어인지 구분하는 머신러닝 모델을 개발했다. 이번 에는 K-최근접 이웃 회귀 모델로 농어의 길이와 무게 데이터로 어떤 농어의 길이만 주어졌을 때 무게를 예측해보자.
분류와 회귀
K-최근접 이웃 회귀에 대해 공부하기 전에, 회귀가 무엇인지 알아보자.
지도 학습 알고리즘은 크게 분류와 회귀로 나뉜다.
분류는 이전 챕터에서 다뤘던 것처럼 말 그대로 샘플을 몇 개의 클래스 중 하나로 분류하는 문제이고,
회귀는 임의의 어떤 숫자를 예측하는 문제이다. 내년도 경제 성장률을 예측하거나 배달이 도착할 시간을 예측하는 것도 회귀라고 할 수 있다.
K-최근접 이웃 회귀라는 이름에서 알 수 있는 것처럼 앞서 공부했던 K-최근접 이웃 알고리즘이 회귀에도 작동한다.
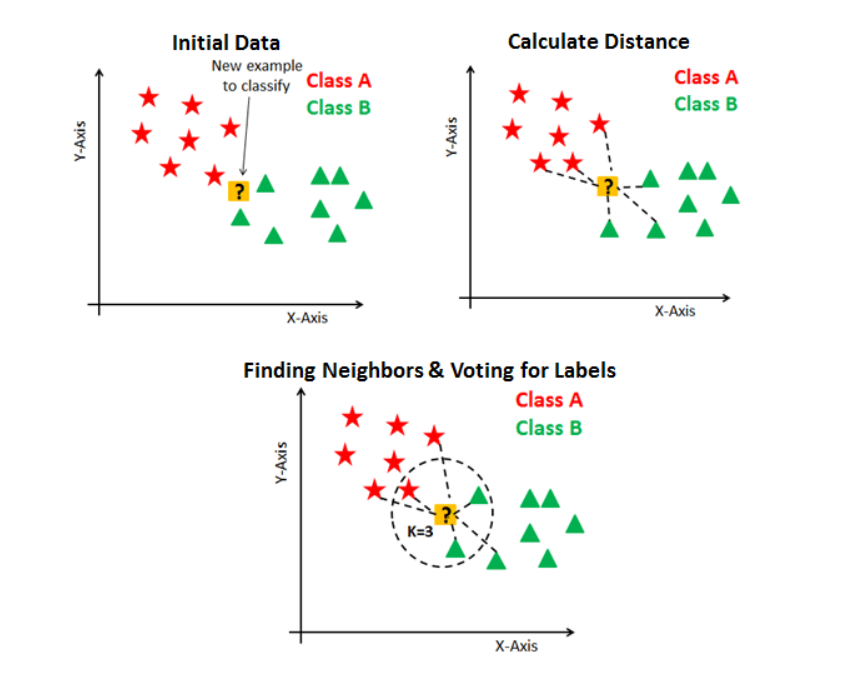
이전 챕터의 내용들이 블로그에는 없기 때문에 간단히 설명하자면, 밑의 그림처럼 특정 샘플이 A인지 B인지 알고 싶을 때 그 주변 샘플들의 거리를 측정하여 가장 가까운 거리부터 순서대로 K개의 클래스를 조사해서 그 샘플이 A인지 B인지를 판단하는 알고리즘이다. K=3인 경우에는 특정 샘플로부터 가장 가까운 3개를, K=5인 경우에는 가장 가까운 5개를 조사할 것이다.
데이터 준비
본격적으로 K-최근접 이웃 회귀에 대해 배워보자.
우리는 농어의 길이를 이용해서 무게를 예측하는 것이기 때문에 농어의 길이가 특성이고 무게가 타겟이다.
import numpy as np
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
1000.0])
import matplotlib.pyplot as plt
plt.scatter(perch_length, perch_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show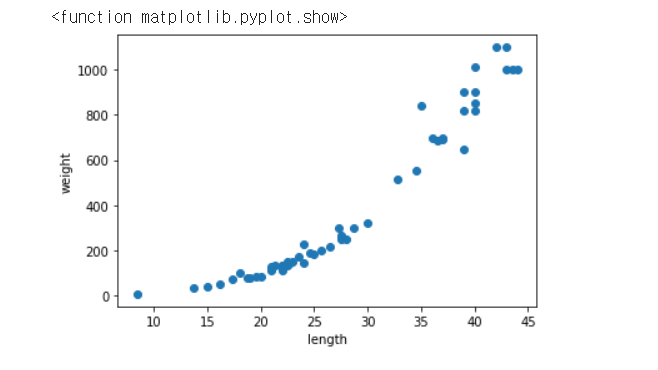
농어의 길이와 무게 데이터로 길이가 커짐에 따라 무게도 늘어남을 알 수 있다. 농어 데이터를 머신러닝 모델에 사용하기 전에 훈련 세트와 테스트 세트로 나누자.
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
perch_length, perch_weight, random_state = 42
)사이킷런에 사용할 훈련 세트는 2차원 배열 이어야 하는데, 위의 train_input과 test_input은 1차원 배열이기 때문에, 2차원 배열로 바꾸어주어야 한다.
파이썬에서 1차원 배열의 크기는 원소가 1개인 튜플로 나타낸다.
예를 들어 [1,2,3]의 크기는 (3, )이다. 이를 2차원 배열로 바꾸면 [[1],[2],[3]]이고 이 배열의 크기는 (3,1)이다.
넘파이 배열은 크기를 바꿀 수 있는 reshap() 메서드를 제공해준다. 연습으로 (4, )배열을 (2,2)크기의 배열로 바꾸어보자.

reshape() 메서드로 test_array가 (2,2)크기의 배열로 바뀐 것을 알 수 있다. reshape() 메서드는 지정한 크기와 원본 배열의 원소 개수가 다르면 에러가 발생한다. 예를 들어 (4, ) 크기의 배열을 (2, 3) 크기의 배열로 바꾸려고 하면 에러가 발생한다.
train_input과 test_input 배열을 2차원 배열로 바꿔보자.
train_input = train_input.reshape(-1,1) #크기에 -1을 지정해주면 나머지 원소 개수로 모두 채우라는 뜻
test_input = test_input.reshape(-1,1) #배열 전체 원소의 개수를 외울 필요가 없다.넘파이는 배열의 크기를 자동으로 지정해주는 기능도 제공한다. 크기에 -1을 지정해주면 배열 전체 원소의 개수를 알아낼 필요 없이 나머지 원소 개수로 모두 채워준다.
결정 계수(R²)
훈련 세트와 테스트 세트를 모두 사이킷런에서 사용가능한 2차원 배열로 변환했으니 훈련을 시켜보자.
사이킷런에서 K-최근접 이웃 회귀 알고리즘을 구현한 클래스는 KNeighborsRegressor이다.
모델을 훈련시킬 땐 KNeighborsClassifier와 같이 fit() 메서드를 이용한다.
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor()
knr.fit(train_input,train_target) #K-최근접 이웃 회귀 훈련
print(knr.score(test_input, test_target)) #결과위 코드의 출력 값인 테스트 세트의 점수는 0.9928094061010639이다.
분류의 경우라면 이 점수는 테스트 세트에 있는 샘플을 정확하게 분류한 개수의 비율이다. 정확도라고 불린다. 다시 말해 정답을 맞힌 개수의 비율이다.
반면에 회귀에서는 예측하는 값이나 타깃 모두 임의의 수치이기 때문에 정확한 숫자를 맞히는 것이 거의 불가능하다.
그래서 회귀의 경우에는 이 점수를 결정계수(coefficient of determination) 또는 R²이라고 부른다.

각 샘플의 (타깃과 예측한 값의 차이를 제곱하여 더한 값)을 (타깃과 타깃 평균의 차이를 제곱하여 더한 값)으로 나눈다. 타깃의 평균 정도를 예측하는 수준이라면 R²은 0에 가까워지고 예측이 타깃에 아주 가까워지면 1에 가까워진다.
타깃과 예측한 값 사이의 차이를 구해보면 어느 정도 예측이 벗어났는지를 가늠하기 좋은데, 사이킷런은 sklearn.metrics 패키지 중에 타깃과 예측의 절댓값 오차를 평균하여 반환해주는 mean_absolute_error를 제공한다.
from sklearn.metrics import mean_absolute_error
test_prediction = knr.predict(test_input)
mae = mean_absolute_error(test_target, test_prediction)
print(mae)mae는 19.157142857142862가 나온다.
이로부터 우리는 예측이 평균적으로 19g 정도 타깃 값과 차이가 난다는 것을 알 수 있다.
과대 적합 vs 과소 적합
위에서 훈련 세트를 훈련시켜 테스트 세트에 적용시켜보았다. 그 결과 테스트 세트의 점수는 0.9928094061010639 였는데, 만약 훈련 세트에 적용시켜보면 어떤 점수가 나올까?
당연히 훈련 세트를 훈련시켰으니 훈련 세트에 적용시키면 테스트 세트의 점수보다 높은 값이 나올 것이라고 예상이 된다.
print(knr.score(train_input, train_target))결괏값으로 테스트 세트의 결괏값보다 작은 0.9698823289099255가 나온다.
이처럼 훈련 세트보다 테스트 세트의 점수가 높거나 두 점수가 모두 너무 낮은 경우에 모델이 훈련 세트에 과소 적합(underfitting) 되었다고 말한다. 모델이 너무 단순해서 훈련 세트에 적절히 훈련되지 않은 경우 이런 현상이 발생한다.
반대로 훈련 세트에서 점수가 굉장히 좋았는데, 테스트 세트에서 점수가 굉장히 나쁘다면 모델이 훈련 세트에 과대 적합(overfitting)되었다고 말한다. 훈련 세트에만 잘 맞는 모델이라 테스트 세트나 새로운 샘플에 대한 예측을 할 때 잘 작동하지 않을 것이다.
그렇다면 위 현상을 어떻게 해결해야 할까?
과소 적합의 경우 모델을 조금 더 복잡하게 만들면 된다. 훈련 세트에 더 잘 맞게 만들면 테스트 세트의 점수는 조금 낮아질 것이다. K-최근접 이웃 알고리즘으로 모델을 복잡하게 만드는 방법은 이웃의 개수 k를 줄이는 것이다.
이웃의 개수를 줄이면 훈련 세트에 있는 국지적인 패턴에 민감해지고, 이웃의 개수를 늘리면 데이터 전반에 있는 일반적인 패턴을 따를 것이다. 사이킷런의 k-최근접 이웃 알고리즘의 기본 k값은 5이므로 3으로 설정하여 출력해보자.
knr.n_neighbors = 3 #이웃의 개수 설정
knr.fit(train_input, train_target)
print(knr.score(train_input, train_target))결괏값은 이전 값보다 높은 0.9804899950518966이 나온다.
테스트 세트도 출력해보자.
print(knr.score(test_input, test_target))결과값은 이전 값보다 낮은 0.974645996398761이 나온다.
테스트 세트의 점수가 훈련 세트보다 낮아졌으므로 과소 적합 문제를 해결한 듯하다.또한 테스트 세트의 점수가 훈련 세트보다 현저히 떨어지지도 않기 때문에 과대적합되었다고 볼 수도 없다.
여기까지 K-최근접 이웃 회귀에 대해 알아봤다. reshape() 메서드로 넘파이 배열을 변경하는 법, 결정계수, 과대적합 그리고 과소적합에 대해 공부했다. K-최근접 이웃 알고리즘과 거의 유사해서 공부하는 데 어려운 내용은 없었던 것 같다.
'AI > 머신 러닝(ML)' 카테고리의 다른 글
| 결정 트리 (Decision Tree) (0) | 2021.08.16 |
|---|---|
| 확률적 경사 하강법 (Stochastic Gradient Descent) (0) | 2021.08.14 |
| 로지스틱 회귀 (Logistic Regression) (0) | 2021.08.11 |
| 특성 공학과 규제 (0) | 2021.08.09 |
| 선형 회귀 (Linear Regression) (0) | 2021.08.09 |
