이전 글에서 농어의 길이 데이터를 이용하여 농어의 무게를 예측하는 K-최근접 이웃 회귀 모델을 구현했다. 앞서 만든 모델을 사용해서 길이가 50cm인 농어의 무게를 예측해보자.
K - 최근접 이웃 회귀 모델의 예측
이전에 사용했던 데이터와 모델을 준비한다.
import numpy as np
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
1000.0])
데이터를 훈련 세트와 테스트 세트로 나누고 reshape() 메서드를 이용하여 2차원 배열로 변환한다.
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
perch_length, perch_weight, random_state = 42
)
train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)
k = 3으로 하는 모델을 훈련시킨다.
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor(n_neighbors=3)
knr.fit(train_input, train_target)
모델을 사용해 길이가 50cm인 농어의 무게를 예측한다.

K-최근접 이웃 회귀 모델은 농어의 무게를 1033g 정도로 예측했다. 하지만 실제 이 농어의 무게를 측정했을 때는 훨씬 더 많이 나간다고 한다. 무엇이 문제일까?
K - 최근접 이웃 모델의 한계
훈련 세트와 50cm 농어 그리고 이 농어의 최근접 이웃을 산점도에 표시해보자. 이전 챕터에서 사용했던 사이킷런의 k-최근접 이웃 모델의 kneighbors() 메서드를 사용하면 가장 가까운 이웃까지의 거리와 이웃 샘플의 인덱스를 얻을 수 있다.
import matplotlib.pyplot as plt
distance, indexes = knr.kneighbors([[50]])
plt.scatter(train_input, train_target)
plt.scatter(train_input[indexes], train_target[indexes],marker='D')
plt.scatter(50, 1033, marker = '^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()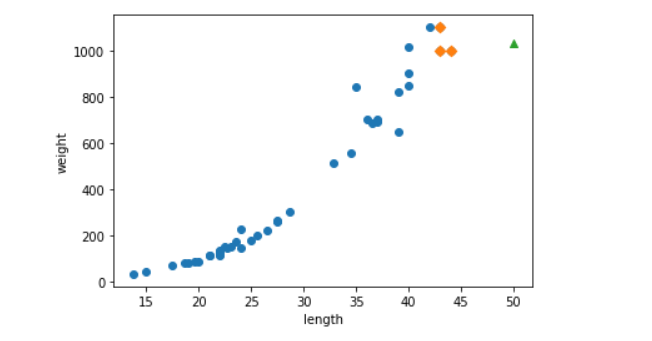
산점도를 보면 길이가 길어질수록 농어의 무게도 증가하는 경향이 있다. 하지만 50cm 농어에게서 가장 가까운 3개의 샘플들은 길이가 45cm 정도이기 때문에 이 샘플들의 무게를 평균하여 50cm 농어의 무게를 예측한다.
이웃 샘플의 타깃의 평균과 50cm 보다 훨씬 긴 100cm의 농어의 무게를 예측해보자.
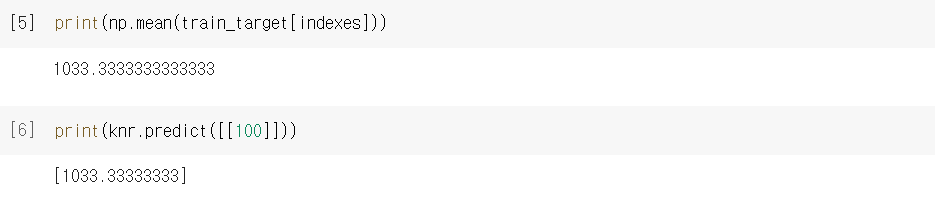
이웃 샘플의 타깃의 평균값은 위에서 예측했던 50cm 농어의 무게와 정확히 일치한다. 또한 길이가 100cm인 농어의 무게의 예측값도 일치한다. K-최근접 이웃 회귀는 가장 가까운 샘플을 찾아 타깃을 평균하여 예측한다. 따라서 새로운 샘플이 훈련 세트의 범위를 벗어나면 엉뚱한 값을 예측할 수 있다.
K-최근접 이웃 회귀를 사용해 이 문제를 해결하려면 가장 큰 농어를 포함하여 훈련 세트를 다시 만들어야 한다. 이 방법이 최선일까?
선형 회귀 (Linear Regression)
선형 회귀는 선형이란 말에서 알 수 있듯이 특성이 하나인 경우 어떤 직선을 학습하는 알고리즘이다.
사이킷런은 sklearn.linear_model 패키지 아래에 LinearRegression 클래스로 선형 회귀 알고리즘을 구현해 놓았다.
사이킷런의 모델 클래스들은 훈련, 평가, 예측하는 메서드 이름이 모두 동일하므로 앞서 사용했던 클래스에서처럼 LinearRegression 클래스에도 fit(), score(), predict() 메서드가 있다.
훈련 세트를 선형 회귀를 이용하여 훈련시킨 뒤 50cm 농어의 무게를 예측해보자.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_input,train_target)
K-최근접 이웃 회귀를 사용했을 때와 달리 선형 회귀는 50cm 농어의 무게를 높게 예측했다. 이 예측값은 어떻게 나왔을까?
선형 회귀가 학습한 직선을 그려보자.
일반적인 직선 방정식은 y = a * x + b처럼 쓸 수 있는데 여기서 x를 농어의 길이, y를 농어의 무게로 바꾼 뒤 데이터에 잘 맞는 a와 b를 찾아서 넣어주면 직선을 찾을 수 있다. LinearRegression 클래스가 찾은 a와 b값은 위에서 선언했던 lr 객체의 coef_ 와 intercept_ 속성에 저장되어있다.

농어의 길이 15에서 50까지 직선을 그려보자. 직선을 그리려면 앞서 구한 기울기와 절편을 사용해서 (15, 15 * 39 - 709)와 (50, 50 * 39 - 709) 두 점을 이으면 된다. (직선을 그릴 때는 plt.plot([a,b], [c,d]) 처럼 배열 안에 두 점을 넣어 사용하면 된다.)
plt.scatter(train_input, train_target)
plt.plot([15,50], [15*lr.coef_ + lr.intercept_, 50*lr.coef_ + lr.intercept_]) #두 점을 이어준다. x 값과 y값은 각각 따로 한 리스트에 넣어준다.
plt.scatter(50, 1241.8, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()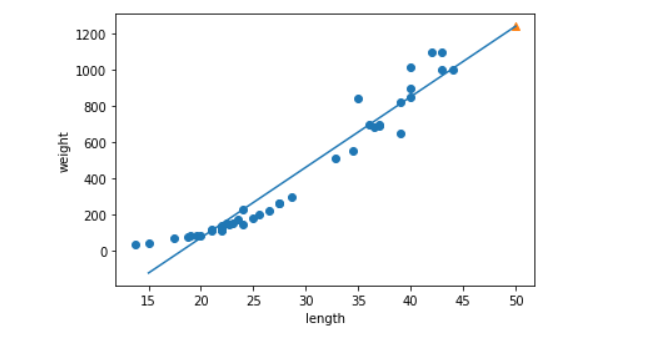
산점도에 표시된 직선이 선형 회귀 알고리즘이 찾은 최적의 직선이다. 길이가 50인 농어는 이 직선의 연장선에 있는 것을 볼 수 있다. 이렇게 우리는 훈련 세트의 범위를 벗어난 샘플에 대해서도 예측값을 찾을 수 있게 되었다.
결정 계수(R²)를 확인해보자.

훈련 세트와 테스트 세트의 점수가 약간 차이가 난다. 그렇다면 이 모델이 훈련 세트에 과대적합되었다고 볼 수 있을까? 사실 훈련 세트의 점수도 높지 않다. 오히려 전체적으로 과소 적합되었다고 볼 수도 있겠다. 게다가 그래프를 보면 농어의 길이가 0에 가까워지면 농어의 무게가 0g 이하로 내려갈 것처럼 보인다.
사실 산점도를 보면 직선에 가깝기 보다는 위로 구부러진 곡선의 형태에 가깝다. 곡선의 일반적인 방정식은 y = a * x² + b * x + c 이므로 길이를 제곱한 항이 훈련 세트에 추가되어야 한다. 넘파이를 사용하면 간단히 만들 수 있다.
이전 챕터에서 사용했던 column_stack() 함수를 사용하여 train_input의 제곱과 train_input 두 배열을 나란히 붙이면 된다. test_input 또한 마찬가지로 붙여주면 된다. 제곱 항을 포함한 훈련 세트를 훈련시키고 예측값을 확인해보자.
train_poly = np.column_stack((train_input ** 2, train_input)) ##column_stack은 두 배열을 일렬로 나열하여 붙여준다.
test_poly = np.column_stack((test_input ** 2, test_input))
lr = LinearRegression()
lr.fit(train_poly, train_target)
직선으로 훈련했던 모델보다 더 높은 값을 예측했다. 이 모델의 계수와 절편을 확인해보자.

이 모델은 y = 1.01 * x² + -21.6 * x + 116.05 의 그래프를 학습한 것을 알 수 있다.
이런 방정식을 다항식(polynomial)이라 부르고 다항식을 사용한 선형 회귀를 다항 회귀(Polynomial Regression)라고 한다.
앞에서처럼 산점도에 그래프를 그려보자.
point = np.arange(15,50) #15~49까지 정수 배열 생성
plt.scatter(train_input, train_target)
plt.plot(point, 1.01*point**2 - 21.6*point + 116.05)
plt.scatter(50, 1574, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()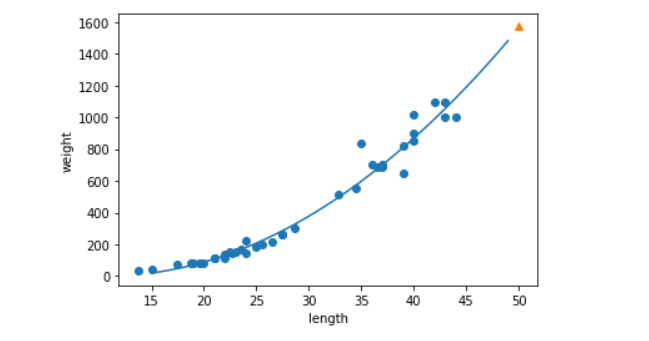
직선을 학습했던 선형 회귀 모델보다 훨씬 데이터에 근접한 모델을 만들었다. R²값도 확인해보자.

훈련 세트와 테스트 세트에 대한 점수가 크게 높아졌지만 테스트 세트의 점수가 더 큰 것을 보니 아직 과소 적합이 남아 있음을 알 수 있다.
다음 글에서는 아직 남아있는 과소 적합을 해결할 방법을 제시한다.
'AI > 머신 러닝(ML)' 카테고리의 다른 글
| 결정 트리 (Decision Tree) (0) | 2021.08.16 |
|---|---|
| 확률적 경사 하강법 (Stochastic Gradient Descent) (0) | 2021.08.14 |
| 로지스틱 회귀 (Logistic Regression) (0) | 2021.08.11 |
| 특성 공학과 규제 (0) | 2021.08.09 |
| K-최근접 이웃 회귀(K-Neighbors Regression) (0) | 2021.08.08 |
